Translate this page into:
Sizing trials of a prototype aircrew helmet: Lessons re-learnt
-
Received: ,
Accepted: ,
Abstract
Aero medical evaluation of a prototype helmet was recently done at IAM, IAF. The aim of the study was to assess the fitment of the helmet and based on the results, to evaluate the suitability of the sizing parameters and the sizing schedule. 44 trained aircrew subjects were asked to select the size of helmet that fit them the best without referring to the sizing schedule. The size selected by the subjects was compared with that recommended by the sizing schedule. The percentage of subjects with two parameter sizing schedule match, one parameter match and no parameter match were calculated. The recorded anthropometric data was statistically analysed to assess the efficacy of the prescribed sizing schedule. Alternate one parameter based sizing schedule was devised using the study data and known data of the IAF aircrew. 34.09% of the subjects selected the same size helmet as recommended by the sizing schedule. 13.6% of the subjects selected a size neither corresponding to head length or breadth as per the prescribed schedule. The rest 51.88% selected a helmet size matching the schedule only in either in head length or head breadth. The one-parameter (head circumference) based sizing schedule was found to be feasible provided statistically derived, suitable thickness inserts were utilized for a better ‘fit’. The multiple parameters used in helmet designing should not be confused with parameters required for the sizing schedules, which need to be simplistic from the user and inventory management perspectives. Sizing of helmets based on head circumference alone satisfies these needs better than the two-parameter based sizing schedule.
Keywords
Sizing trials
Prototype aircrew helmet
Head circumference
Introduction
Proper sizing and fitment of a helmet is an important consideration in effective protection of the aircrew from head injuries. With increased use of Night Vision Goggles (NVG) and Helmet Mounted Display Systems (HMDS), the optimal fitment of helmet on which these devices are mounted has become even more critical to preserve optimal in-flight vision. The extreme complexity and variability of head geometry exaggerates the inherent limitations of individual anthropometric dimensions such as head length, breadth, height and circumference.
The conventional basic principle in flying clothing design includes use of anthropometric parameters as relevant to the body part on which the flying clothing is likely to be used. These anthropometric parameters are then converted to relevant sizing parameters and sizing rolls of various sizes are developed that would comfortably fit the entire target population. The sizes planned in the sizing rolls should ideally cover the entire range for the user population and yet divide it in equal parts for the sub-sizes so that the logistics of demand and supply of various sub-sizes is simplified. The prototypes developed as per the proposed sizing rolls are then further evaluated by ‘fitment trials’, which are done on a sample of subjects drawn from the target user population. Based on the inputs of the sizing trials, the sizing rolls are fine-tuned.
Since the various areas of the human body on which the flying clothing is going to be worn is 3-dimensional, ideally all sizing schedules would need at least three parameters that best represent each of the 3 dimensions and are anthropometrically orthogonal (minimal correlation between them) to each other. However, research has shown that in mass designing of flying clothing (vis-à-vis individual customised designing) by increasing the number of sizing parameters the satisfaction of fitment decreases [1] (Fig. 1).
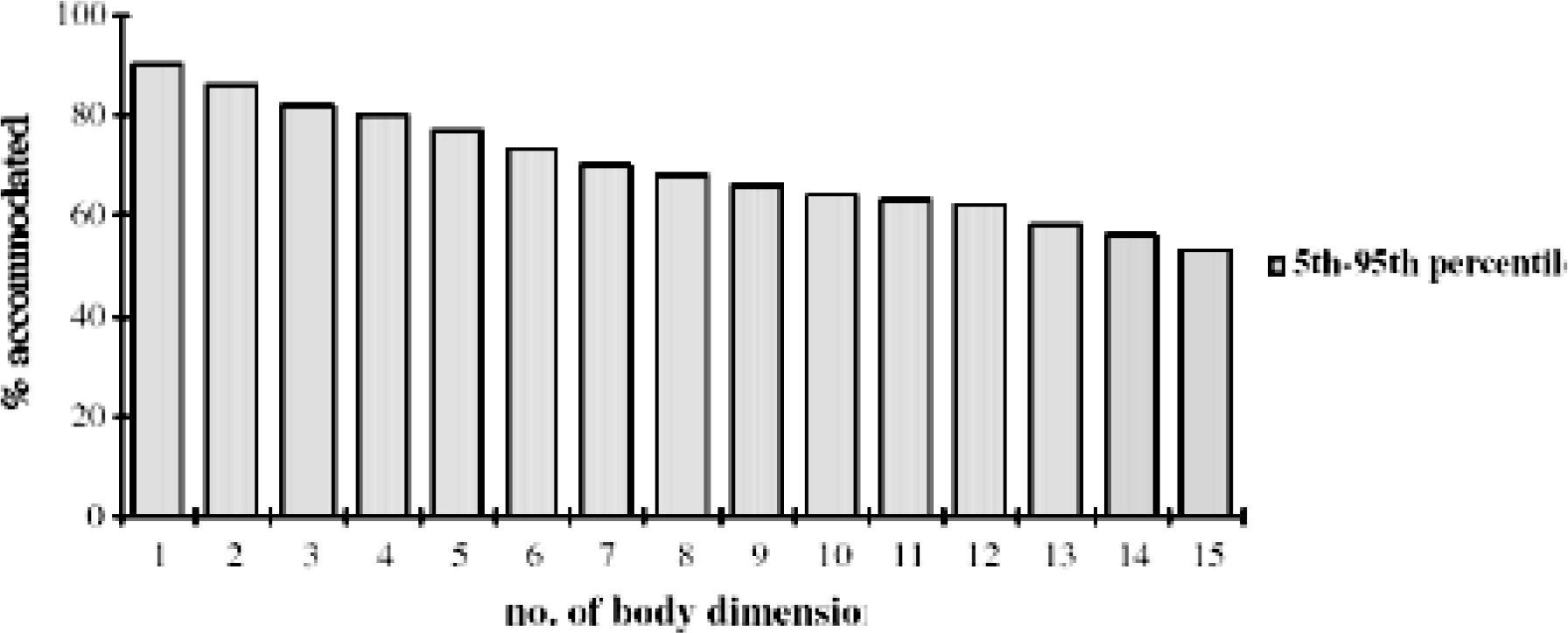
- Number of Sizing Parameters vis-à-vis % Fit of population
Moreover, greater the number of sizing parameters, greater number of sizes would be required to cater for variability of all the parameters in the population. Let us say that the variability of each parameter in the population is covered by dividing in three equal parts. If one sizing parameter is used, then entire range of that anthropometric parameter in the population can be covered in 3 sizes. However, if two sizing parameters are used, then the number of sizes required would increase to nine; which would include having three sizes using the first parameter with three sub-sizes in each based on the second parameter.
Flying helmets are unique due to the shape of the head where in all the three dimensions (represented by head length, head breadth and head height) are significant to ensure ideal fit. Each human is shaped differently. Not all narrow heads are short in height and not all wide faces come with wide heads. Designing to the average head and then simply scaling that head larger or smaller in all dimensions (‘Percentile Man’ concept), will produce a size roll that fails to accommodate large segments of the population [2].
A review of the in use operational helmets in the Indian Air Force (IAF) brought out that head circumference is more commonly as a single sizing parameter for sizing vis-a-vis head length and head breadth combination which is being used only in ZSH 7 helmet [3]. The helmet sizes and inserts based on head circumference used in IAF are shown in Table 1 [4, 5, 6].
| Sl No. | Helmet | Sizes | Insert sizes |
|---|---|---|---|
| 1. | Gallet (NVG in helicopters) | XS, S, M, L, XL, XXL | 5 mm to 15 mm |
| 2. | Gueneau type 458 (Mirage 2000) | 7,0,8 | Three sub-sizes depending on inserts |
| 3. | MK 3C/4A (Jaguar) | Small, medium, medium b road and large | Nil |
| 4. | ZSH 3 (MiG series) | Outer shell :1 and 2Inner helmet : 8 sizes | Nil |
| 5. | Alpha 300 ( Hawk) | Small, medium, medium broad, medium long large | Crown and brow padding of 3 sizes 6, 9 and 12 mm |
An aero-medical evaluation of the prototype of a new helmet was recently carried out at the Institute of Aerospace Medicine (IAM). As part of the aeromedical evaluation, the prescribed sizing schedule for the helmet was tested with fitment trials. The aims of the fitment trials were to assess the fitment of the helmet on a sample population of the Indian aircrew and to comment on the suitability of the prescribed sizing schedule and the sizing parameters chosen.
| Sl No. | Size | Designer sizing schedule | |
|---|---|---|---|
| Head length (cms) | Head breadth (cms) | ||
| 1 | Small | 17.3 – 18.4 | 13.7 – 14.7 |
| 2. | Medium | 18.7 – 19.6 | 14.5 – 15.7 |
| 3. | Medium Broad | 18.2 – 19.6 | 15.1 – 16.0 |
| 4. | Medium Long | 18.9 – 20.0 | 14.5 – 15.7 |
| 5. | Large | 19.4 – 20.3 | 15.5 – 16.3 |
Study Design
The prototype helmet consisted of an outer helmet shell with soft inserts. Three basic helmet shells were prepared and fitted with fixed inserts to create 5 sizes. The sizing schedule by the designer prescribed five sizes, viz. small, medium, medium broad, medium long and large, based on head length and head breadth. The sizing schedule provided is shown in Table 1. Additional removable inserts designed to cover the top and sides of the head (like a skull cap excluding the ear cups) were provided in three thicknesses, viz.10, 15 and 20 mm. The 10 mm insert was the factory fitted default for all the sizes and if need was felt, it could be replaced with either 15 or 20 mm insert.
The assessment of fit of the prototype helmet in trained aircrew employed a double blind trial design. 44 aircrew subjects, all trained test pilots, were measured by standard anthropometric techniques for head length and head breadth using callipers. Their head circumference was measured using a measuring tape. The least count for all parameters was 0.1 cm. The aircrew were asked to select the size of the helmet that fit them best by trial and error without referring to the prescribed sizing schedule (i.e. first blinding). The ‘fit’ on the aircrew was also assessed by the Aviation Medicine specialist for ease of donning and doffing, slippage/ play after strapping, position of ear cups and presence of pressure points or ‘hot spots’ without referring to the sizing schedule (i.e. second blinding). The size of helmet selected by the aircrew was noted. The data was subsequently analysed for Percentile distribution of the three parameters with test of normalcy. Also comparison of the size chosen by aircrew vis-a-vis that prescribed by the sizing schedule was done.
Results and Discussion
The three measured parameters of head circumference, head length and head breadth were evaluated for normalcy using the D’Agostino-Pearson normality test and found to follow normal distributions. The sample used in the study was hence well representative of the target population, i.e. Indian military aircrew.
All the aircrew were able to select one size or the other using trial and error method. Only one aircrew required the vertex padding to be changed to 15 mm for a better fit. The percentage of various sizes of helmet used by the subjects is shown in Fig. 2. The graph clearly shows that the usage of various sizes of helmets is highly unequal despite the sample being well representative of the population. The medium long size would be used by more than half the subjects and the large size by another quarter of the aircrew. The medium and medium broad would be used by 8.7% and 6.5% aircrew respectively and the small size may not be required at all.
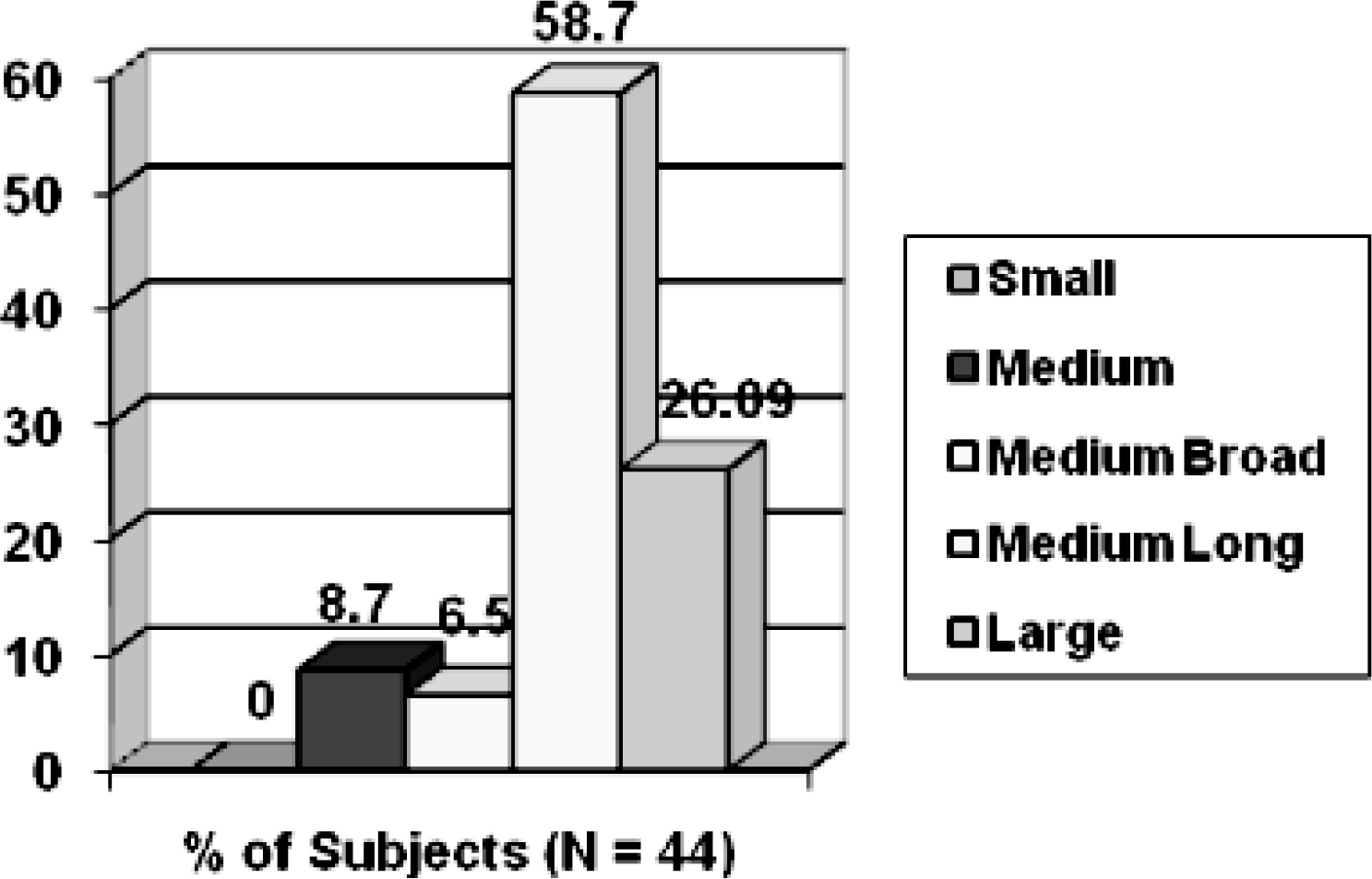
- Percentage of Various Sizes of Helmet used by the subjects
The selected size was compared to that prescribed by the recommended sizing schedule based on head length and head breadth. Fig. 3 shows the percentage of subjects in whom both parameters matched the chosen size, either of the parameters matched the chosen size and none of the parameters matched the chosen size. It was found that only 34.09% subjects selected a helmet size that correctly matched their head length and head breadth as prescribed in the sizing schedule. In 13.6% of the subjects the selected size of helmet corresponded to neither the head length nor head breadth prescribed in the sizing schedule. This indicated that the sizing schedule did not cater for or incorrectly catered for the peculiar head geometries of these subjects. Out of the rest, 27.27% selected a size matching the schedule in head length only and 24.61% selected a helmet size corresponding to the schedule in head breadth only. This indicated that for 51.88% subject in whom only one sizing parameter matched, there was another size of the helmet which could also have been used as per the sizing schedule.
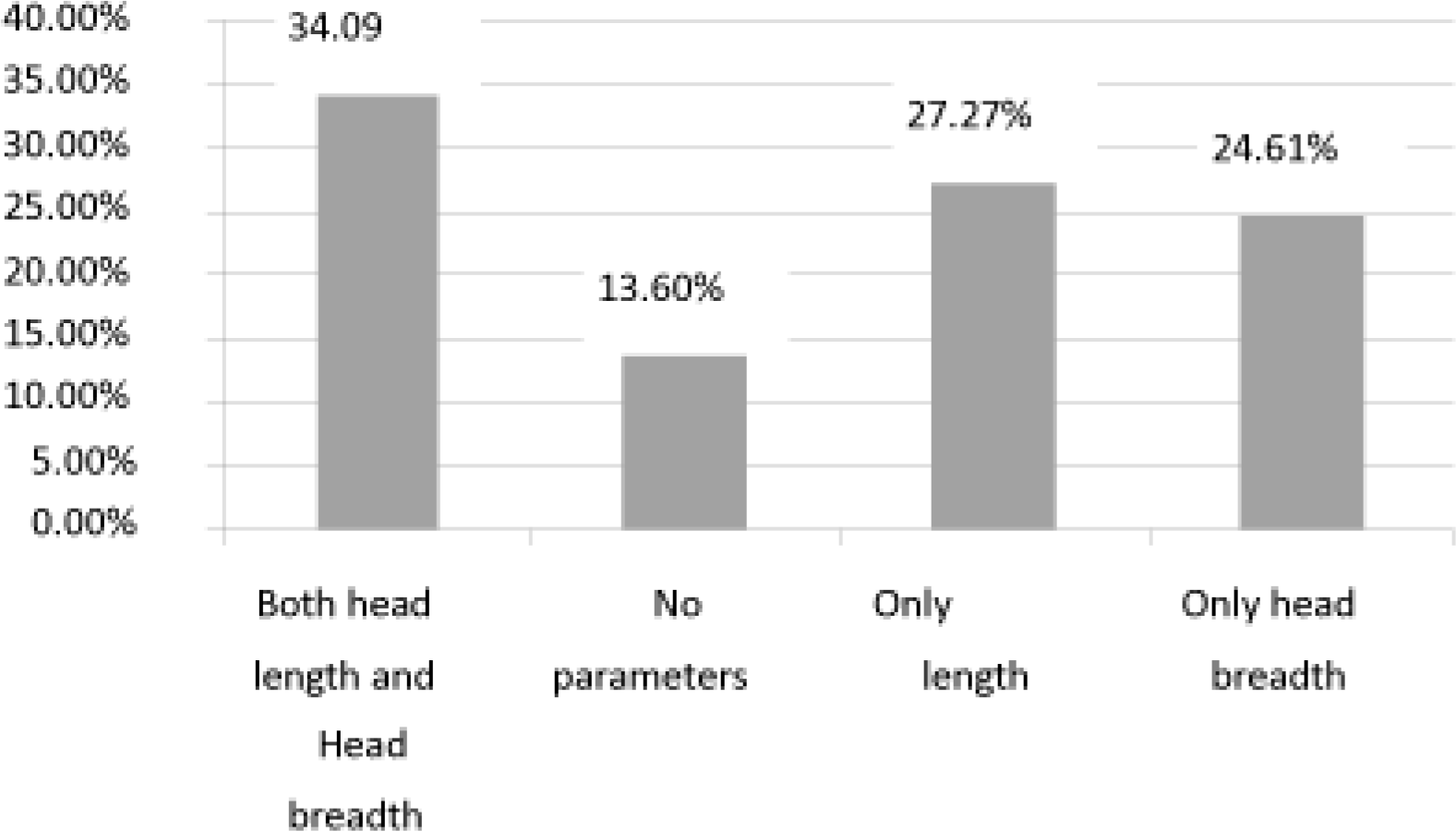
- Percentage distribution of Fit of test subjects
Although the various helmet sizes achieved 100% during the trials, the salient observations have serious implications in sizing, fitment and procurement. A large number of aircrew in the field, some of them not as experienced as used in the present study, would have to resort to unscientific trial and error method in choosing the correct helmet size rather than choosing the correct helmet based on the sizing schedule. The logistics of procurement of correct sized helmet cannot be ensured leading to possible shortages of right sized helmets. This in turn may lead to selection of ill-fitting helmets by the aircrew.
An effort was hence made to understand the specific reasons for the discrepancy between the size prescribed by the sizing schedule and that selected by the subjects. A bi-variate analysis of the head length and breadth parameters was carried out and is depicted in Fig. 4. Using a 95th percentile box it was found that the outliers and the borderline subjects corresponded with the subjects who had selected a size other than the prescribed values.
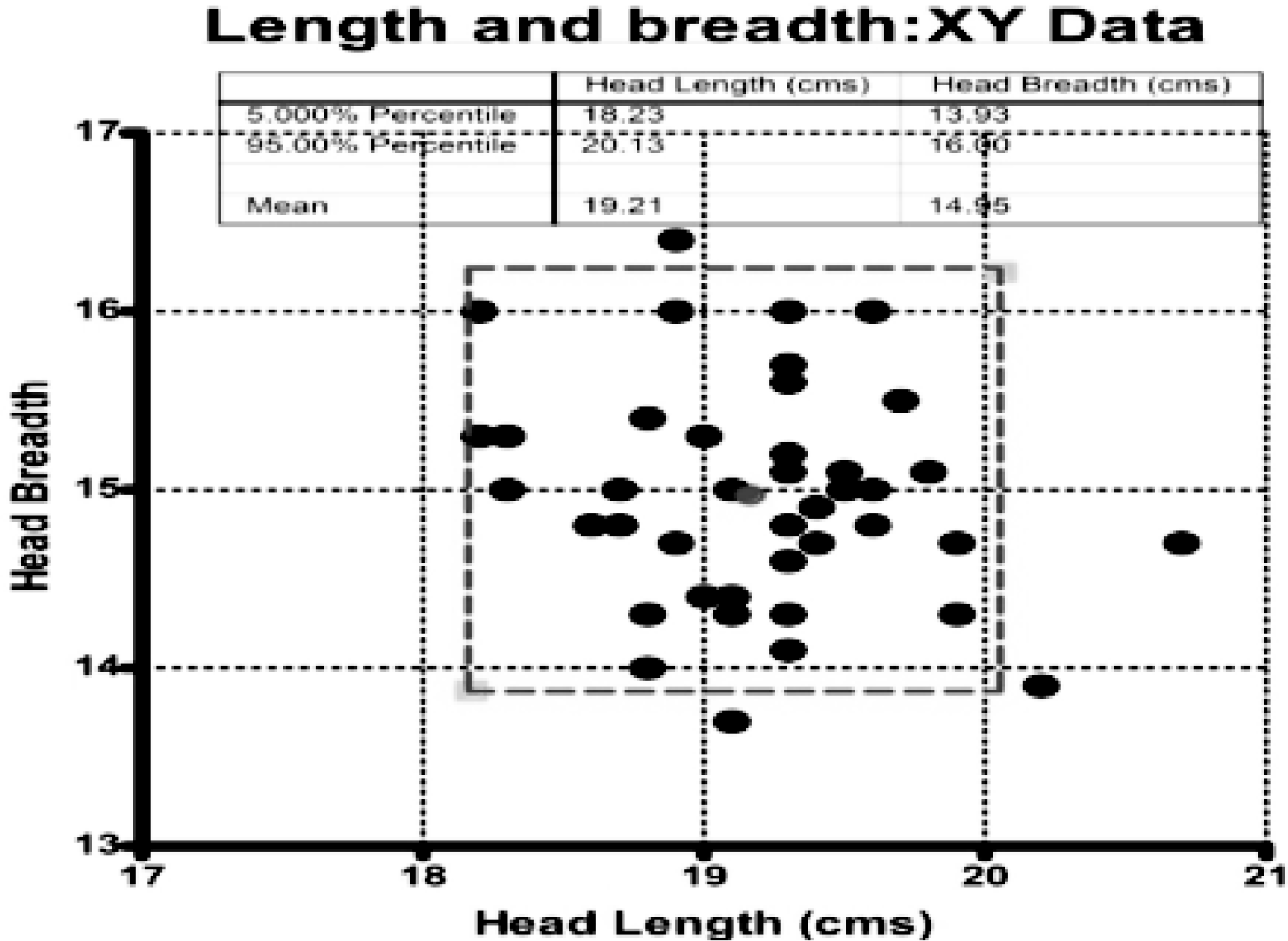
- Bivariate analysis oh hl hb 5-95 5box showing outliers
An evaluation of the Kurtosis of the measured head length and head breadth of the sample was done. The Kurtosis for head length was found to be 0.81 and that for head breadth was found to be - 0.12. This is depicted graphically in Fig. 5. This means that the head length has a more peaked distribution and the head breadth has a more flat distribution than the normal. Since the Kurtosis is different, the sizing schedules with equal width distribution for both head length and head breadth cannot cater for the population when both parameters together constitute the sizing schedule.
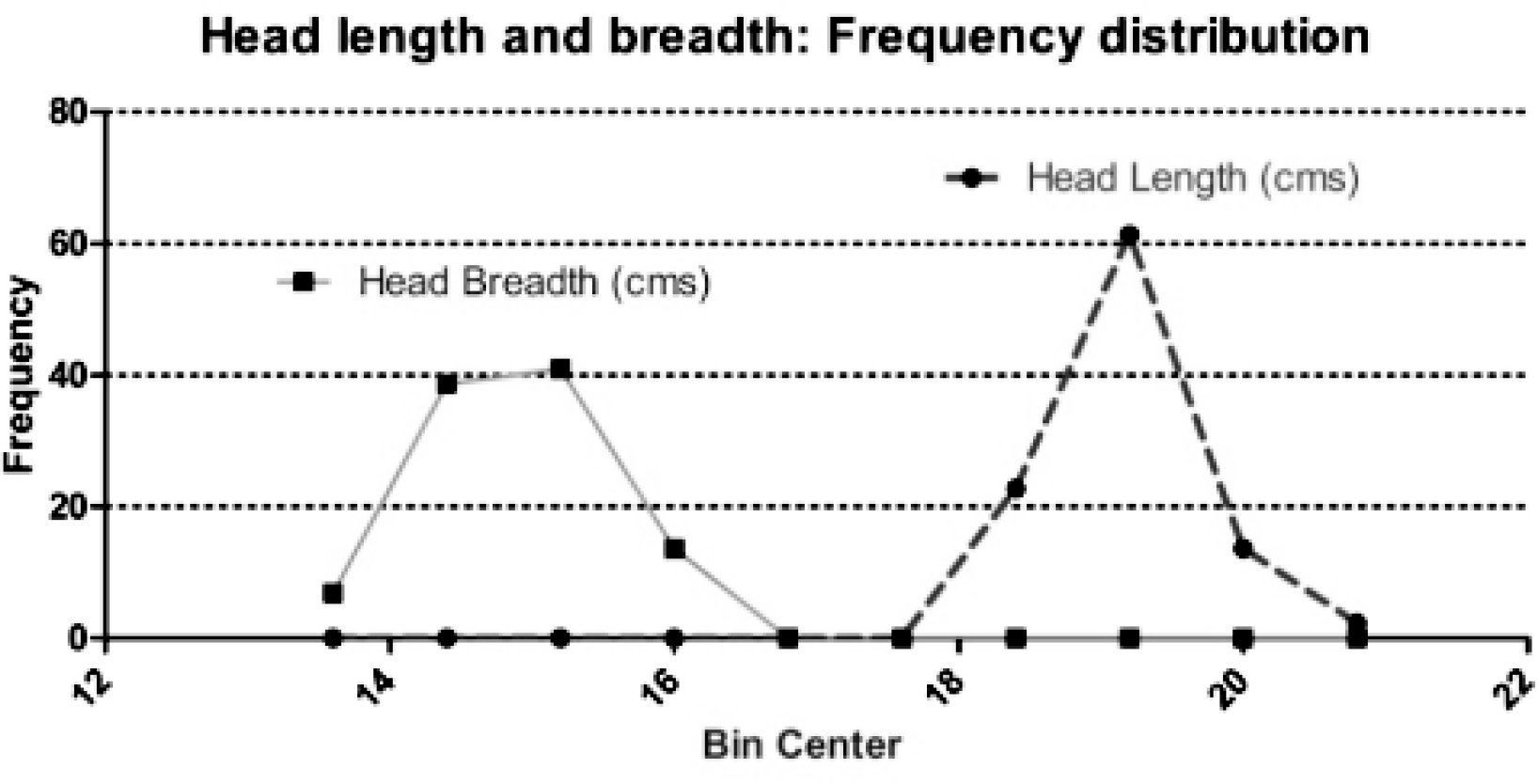
- Distribution of Head length and head breadth parameters showing difference in kurtosis
The anthropometric database used by the designer was also scrutinized to understand the reasons for the observed defect in the prescribed sizing schedule. The designer has used the data collected under the DIPAS project RD-P1-2003/ DIP-243 [7]. The head length and head breadth (like all other recorded parameters), are available as ‘minimum’, ‘maximum’, ‘5th percentile’, ‘50th percentile’ and ‘95th percentile’ values. From these five values the designer had extrapolated the complete percentile distribution using statistical approximation techniques. The percentile distribution so achieved has subsequently been used to devise the sizing schedule. The scientific validity of such approximation is debatable. Ideally, first the consistency of the raw data should be ascertained and then the actual percentile tables derived.
Thus, it was considered essential to re-visit the issue of devising a helmet sizing schedule denovo for the IAF aircrew. The various principles in devising helmet sizing schedules are enumerated.
‘Goodness of fit’. The ‘goodness of fit’ of a particular size of a helmet is inversely proportional to the anthropometric range accommodated within that size. The ‘within a size’ variation is large when the sizing intervals are broad.
Number of sizing parameters. When using a two key dimension sizing schedule with each dimension having three intervals, the ideal total number of sizes would be nine, but the three intervals would have a large within-size variation. In comparison, when using a single key dimension sizing schedule, the total number of sizes can be increased to five and achieve lesser within-size variation. Such a strategy has proven to have a better ‘goodness of fit’ [2].
Ideal single parameter. Since head circumference combines the head length and head breadth, it is shown to be a good representative of the variations in these orthogonal parameters. The variations in head breadth and length will be readily accommodated as long as sufficient room is provided in the shell to accommodate the statistically derived liners or inserts to ensure proper fit. Moreover, measuring head circumference with ordinary tape has been shown to be less erratic than measuring head length and breadth using specialised callipers, which also requires specially trained personnel.
Design of inserts. A given value of head circumference (i.e. a given size) may have different head lengths and head breadth. To accommodate for these variations and achieve higher ‘goodness of fit’, the ‘Standard Error of Estimate’ of these two parameters for that size is recommended to be used in design of inserts to be placed as per individual requirement. The Standard Error of Estimate is given by the formula [2]
SE = Standard error of estimate
y = Head length/ head breadth of the population within the given size
SD = Standard deviation of head length/ head breadth of the population within the given size
r = Correlation coefficient between head length/ head breadth and head circumference within that size.
The standard error of estimate is calculated for each size separately for head length and head breadth. The final thickness of inserts is determined by approximating the statistically derived values to the nearest mm. The inserts are to be suitably placed by individuals’ users during fitment: occipital/frontal to correct for head length and temporal to correct for head breadth.
Based on the basic principles of devising a sizing schedule for aircrew helmets discussed above, a sample head circumference based sizing schedule was devised for the IAF aircrew. Since the DIPAS data was insufficient as discussed above, the anthropometric head geometry data (head length, head breadth and head circumference) was taken from IAM Departmental report IAM/TR/136/2007, which is available in form of descriptive statistics and percentile distribution. A pertinent observation is that the DIPAS data did not include data of the flight cadets of the IAF. Therefore on this account, the IAM data which includes entry level data for the flying cadets is more suitable in designing a helmet schedule for an aircraft to be used as a trainer. The statistical analysis of the three parameters in this database is shown in Table 3. This indicates that the data is consistent, usable and representative of the population in so far as head circumference is concerned. The data also shows that head circumference has lesser skewness and kurtosis, possibly an indicator of easier measuring technique by a simple tape than the other two parameters that are measured using specialised callipers. It is pertinent to note that this was also reported by Zeigen et al [2].
| Sl No. | Values | Head circumference | Head length | Head width |
|---|---|---|---|---|
| 1 | Number of values | 498 | 463 | 473 |
| 2 | Minimum | 50 | 16 | 13 |
| 3 | Maximum | 61 | 23 | 19 |
| 4 | Mean | 55 | 18 | 15 |
| 5 | Std. Deviation | 1.7 | 0.92 | 0.71 |
| 6 | Std. Error | 0.075 | 0.043 | 0.033 |
| 7 | D’Agostino & Pearson omnibus normality test K2 | 1.8 | 7.8 | 34 |
| 8 | P value * | 0.3986 | 0.0200 | < 0.0001 |
| 9 | Passed normality test (alpha=0.05)? | Yes | No | No |
| 10 | P value summary | ns | * | *** |
| 11 | Skew ness | -0.036 | 0.13 | 0.37 |
| 12 | Kurtosis | 0.30 | 0.72 | 1.9 |
* A small p value is evidence that data was sampled from a non-Gaussian distribution. A large p value means that data are consistent with a Gaussian distribution
The sizing schedule for the helmet so devised is shown in Table 4. A schedule for the thickness of inserts to cater for head length and head breadth variation to be used for each helmet size has also been devised using two standard errors of estimate as extreme values. (Table 5)
| Sl No. | Size | Head circumference | Predicted % of population fit |
|---|---|---|---|
| 1 | Sub-small | 51.75 – 53.12 | 13.65 |
| 2 | Small | 53.12 – 54.49 | 15.46 |
| 3 | Medium | 54.49 – 55.86 | 31.12 |
| 4 | Large | 55.86 – 57.23 | 29.31 |
| 5 | Extra large | 57.23 – 58.60 | 7.02 |
| Sl No. | Size | Liner/ insert | thickness (mm) |
|---|---|---|---|
| 1 | Sub-small | 6 | 12 |
| 2 | Small | 6 | 12 |
| 3 | Medium | 7 | 14 |
| 4 | Large | 6 | 12 |
| 5 | Extra large | 6 | 12 |
standard error of estimates in head length and head breadth.
This five-size schedule devised using the available anthropometric data was retrospectively applied on the data of the 44 aircrew subjects used in the fitment trials. It was statistically found that this sizing schedule would accommodate 98% of this test population.
In lieu of a single insert, multiple inserts to achieve even better fit, as has been done in designing the Gallet helmet (used for NVG operation), can be used [5]. Additional inserts on top of the head to accommodate for the variation in vertex height can be designed using the statistical principles discussed earlier.
Not withstanding the best design efforts, the importance of ‘fitment trials’ of any helmet are considered mandatory to cater for extreme individual idiosyncrasies that cannot be approximated by statistical techniques.
The ideal technique for the helmets whose ‘fit’ is absolutely critical e.g. HMDS, is to customise the mould of the inner helmet to individuals’ head [8]. Once the head mould is prepared, the inner shell is designed to the mould and the outer shell is constructed over it. Such a technique provides a larger surface area of the helmet in contact with the head, which makes the helmet a more stable platform for mounting HMDS. This also achieves a better weight distribution to reduce the potential for pressure points. A moulded helmet system may also guarantee the reproducibility of a good fit without the need for periodic readjustment [9]. In India, the first steps towards individual customisation of the helmet have now been initiated with the induction of HMDS in the LCA program [Personal communication].
Conclusion
Anthropometric choice of key dimension for use in helmet fitment is a critical feature of the helmet sizing schedule. A clear distinction needs to be made between the multivariate parameters required for accurate designing of a helmet and the simplest possible parameter for sizing and fitment. A ‘five-size’ schedule using the parameters of head length and head breadth has been found to be unsatisfactory during the user trials. Use of head circumference as a single sizing parameter along with suitable inserts is a better alternative. Though the actual ‘goodness of fit’ would need to be determined by user trials, the ease of sizing and fitment in the field and simpler logistics and procurement procedures make head circumference based sizing schedule a preferred option.
Conflict of interest: None
References
- Digital human modelling for virtual fitting trials In: Nordic Ergonomics Society Conference Proceedings. Iceland: Loughborough University Reykjavik; 2008.
- [Google Scholar]
- A head circumference sizing system for helmet design In: Wright- Patterson AFB, OH: Wright Air Development Division, Aerospace Medical Division. 1960. WADD Technical Report 60-631
- [Google Scholar]
- LH 050 / 150 /250 Flight helmet instruction manual. CGF Gallet. [Accessed on 2009 Sep 18]. Available from: http://www.flighthelmets.com.au/manuallh.PDFs
- [Google Scholar]
- Anthropometric considerations in design and development of an Indian flying helmet In: Defence Bioengineering and Electromedical Laboratory. 2004. DEBEL technical report No. DEBEL/TR/04
- [Google Scholar]
- To study the various flying clothing assemblies and their sizing in use in the fighter aircraft of IAF. Field project in Aviation Medicine.
- [Google Scholar]
- Body measurements: Design application and body composition In: Defence Institute of Physiology and Allied Sciences, Delhi. 2003. DIPAS Project No. RD-P1-2003/DIP-243
- [Google Scholar]
- Determining aircrew helmet size design requirements using statistical analysis of anthropometric data. Aviat Space Environ Med. 1991;62:67-74.
- [Google Scholar]
- Principles of fit to optimize helmet sizing. 2005. In Strategies to Maintain Combat Readiness during Extended Deployments–A human systems approach. :6-1-6-16. Meeting Proceedings RTO-MP-HFM-124, Paper 6. Neuillysur-Seine, France: RTO. [Accessed on 2009 Sep 18]. Available from: http://www.rto.nato.int/abstracts.asp
- [Google Scholar]






